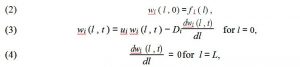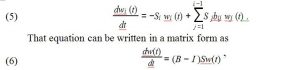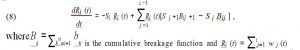BALL MILLS
- Low maintenance and operation costs
- High capacity
- Very easy maintenance terms
In order to grind and crush different kinds of dry and wet materials, such as minerals, construction materials, sand and cement, lime and ceramic materials, the best way is to use Ball mills.
Engineers ….. With years of useful work experience, have been able to design and market this device. The Horizontal Ball mills Device has now been recognized as a fully trusted machine for grinding plants.
The main characteristics of the balloons that work with the type of shoe bearings:
• costs operating and maintenance is low
• Totally reliable
• High capacity
• Made in smaller space compared to mills trunnion bearings base
Internal structure of Mill:
- Armored exterior
- Classified diaphragm
- External wall
- Grinding charge
Structure of Ball mill
Shell of mill
At the first we bent and welded Partitioned plates together.They have then been heated to a high pressure in order to strengthen these parts. After that, the entire body of the device is inspected by non-destructive testing. Machine and bearings of the mill have been tested with great care on the ground in order to be sure of accuracy.
Place of Mill
Shoe-type bearings are made on oscillating parts that seated on oscillating sweeping blades and designed with dynamic hydraulic fluid lubrication. They are designed to easily fit the shape of the rings in their hearts and fit them. Our engineers also provide mills with a classic design on trunnion bearing.
Milling gear
The mill is powered by a central propulsion system with the help of a DMG 2 gearbox, with two gears and a gearbox, a smaller gear for the mill and a countershaft. The device also has an auxiliary drum that is used at the time of the original drum failure.
Two-part mills
Two parts mill or Two chamber cement mills are used for crushing and milling cement, iron cement and other similar materials. These two parts are embedded in a high-performance VTP. According to Blaine’s view, these mills can pour up to 6500 cm2 /g. The mill itself is equipped with an armored lift in the first part, which has larger mills with higher grinding power. In the second part, smaller mills are used to finish milling.
The classified diaphragm have a material control sensor, so that a certain amount of material can be crushed in both parts of the mill. The materials that are in the upper mill are molded by an external wall to a separate section. If the material is hot, it is sprayed into two rooms by water sprays for cooling. If the mill has a pressed drive or roller, one-piece mills are classified with an armored classification without aperture.
Mills of one or two raw material compartments with a pre-dryer chamber
For grinding materials for use in kiln lines, one or two compartments mills with a pre-dryer chamber are used. This kind of mill has a circuit and has a high efficiency VTP separator that separates materials for drying using a furnace gas or a heat from a cooling chamber. This kind of grinding is due to materials that have a moisture content higher than 8%. The material removed from this device is as small as 12÷14% R90 crushed and moisture less than 0.5%.
All materials are first placed in a drying enclosure to dry properly before entering the damper area. In this section, the finer materials are separated and the coarser materials are directed towards the mill. seating and drives that are exactly similar to cement mills are also used for this device.
Pneumatic mills
This type of mill has a pre-mill dryer and only a one milling compartment. Materials are placed on the floor of the mill and then directed to the high quality LRT separation unit. Finally, the product collects in a filter or cyclones. Typically, pneumatic mills are used to grind very wet materials.
In this machine, high-temperature with a large volume drying operations are performed using a gas blown to the dryer, mill, and separator compartment. The popularity of the pneumatic mill is due to its simple and reliable design. Materials that are mined by the Pneumatic Mill are designed to grind coal and petroleum coke in a high-performance LTR-U separation medium with a pressure drop of over 3.5 times.
Mills seated on trunnion bearings
Our engineers have designed a large number of ball mills with a unique and classic design on swing trunnion bearings.
ball mill
In this paper, we intend to discuss the latest methodology and practices in the field of modeling and controlling the grinding process in the Ball mills. Although this paper focuses mainly on basic kinetic and the energy models of the mill process, we will continue to described and analyzed more available control strategies.
Keywords: Process control, Ball mill, grinding circuit
- Introduction
One of the most advanced and best methods for grinding and reducing the size of different particles with different nature and specific physical, chemical, and mechanical characteristics is the use of the most important technology of Ball mills in various industries.
Perhaps most commonly referred to as materials such as ores, minerals, limestone, etc., which are converted to smaller sizes by using ball mills. But in general, the large use of ball mills in various industries, including mining and mineral industries, metallurgy, processing and cement production, in various chemical industries, in the pharmaceutical industry and cosmetics industry, in the production of ceramics, in many different studies of science Laboratory and all kinds of tests are used.
Of course, ball mills are not only used for crushing and reducing the size of different materials into smaller sizes, and in many industries these ball mills are also used to blend, mixed, disperse, amorphous materials physics, or even mechanical alloying will be exploited.
Structurally, the ball mill includes a cylindrical vessel that is carefully mounted or fitted to the two ends to allow rotation around the central axis to be easily provided. The mill is connected to the shell by a girth gear and a pinion shaft drives it with the prime mover.
Commonly used synchronous motors that are equipped with an air clutch or a transfer gear are usually used as prime movers. After that, mill usually charged with raw materials such as ore, stone, etc., and grinding media are also prepared using balls.
By moving the kinetic energy of the grinding media to the product needed for the mill, the grinding process is performed during a rotary movement.
Typically, the ball mills have a wide range of variations, and their design is based on issues such as size, equipment used for loading raw materials (feeders), and even the discharging the output product system. Accordingly, the size of mills is usually determined by the ratio “length to diameter”, which is often found between 0.5 and 3.5.
To load raw material, it can be done either using a spout feeder or using a means of a single or double helical scoop feeder.
In terms of discharge system, ball mills are different and have different types. Therefore, in terms of discharge system, ball mills can be classified as overflow discharge mill, diaphragm or grate discharge mill, and center-periphery discharge mill.
Usually, for industrial applications, mills are used with the inner surface, and the steel body of the grinder and all types of suitable milling equipment are used depending on the industry, so that the contents of the mill can be reached with the best possible weight to prevent falling or dropping or cascades down.
Generally, in the ball mills, there are generally three types of grinding media that these three types of media are:
- Types of metal balls like steel balls
- Different types of cylindrical metal known as clypeus
- Different ceramic balls made of high density or orderly.
The standard size of the balls is in the range of 10 to 150 millimeters in diameter depending on the type of mill, and the material used to supply these balls for grinding media is often steel and other types of other metals.
The Cylpebs structure has a slightly conical shape in the cylinders of a grinding cylinder, the edges of which are rounded, and its length and diameter are considered equal, with different dimensions considered to be between 8 x 8 to 45 x 45 mm depending on their usage.
Due to their high density and specific surface area, they have developed their shape in order to maximize the productivity of grinding.
The porcelain balls are usually regular dense ceramic balls, while using the oxidized aluminum in the ball structure, they produce high-density balls to withstand higher wear resistance.
The mass and size, ware rate, the impact on the rate of expansion failure and the efficiency of grinding energy are the main features and basic properties of the milling bodies.
The three basic types of operating modes of the grinding machine are determined by the speed of the machine: the low speed of rotation (cascading), the fast speed of the rotation (cataracting), and the very high speed of rotation or ultrafast rotation (centrifugation). Each of these speeds has a special trajectory of motion charging path in the mill, which has different effects on the material on the ground.
In addition, the process of milling will be different to other factors, such as dry or wet conditions, or that the moist materials are added to the starting material during the milling process. In this paper, different grinding dimensions in dry conditions and wet conditions of materials are also mentioned.
Generally, the reduction in the particle size in the mill depends on a number of factors, most important of which are:
- Some materials specifications such as mass, volume, hardness, density, charge size, and other specifications of materials that are charged to the mill
- Features such as mass, density, and ball size distribution in grinding media
- The rate of speed rotation of the mill
- The amount of Slurry density in the wet mill operation
In the following, you can get some estimates of these parameters.
One of the most important characteristics of a ball mill is the amount of production or amount of material that these mills can produce per hour, which is usually measured s amount of ton production per hour. Of course, the capacity of industrial ball mill production is due to several factors such as mill size, type of grinding structure (overflow or grate discharge), speed of rotation, milling load, final product size required according to feed size (coefficient of reduction) Material, ability and power of the shaft of the mill and even the gravity of the material.
In this paper, we have tried to carefully examine all of these parameters and suggest an empirical relationship that takes into account the capacity of the mill as the ratio of power to the shaft and the amount of energy consumed in the grinding process.
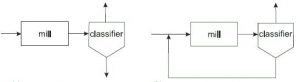
To achieve the best particle size, considering that milling in an environment and industrial conditions is usually works in grinding circuits that in a condition and process that has already been done to classify the materials based on their size. In Figure 1, the simplest cases of open and closed circuit are well illustrated.
Fig.1
In the first case, all output materials are separated in the same parts in different sizes, and therefore the classification does not affect the grinding process. In the second case, coarse materials are returned to the mill feed by the classifier and finally the desired output product is taken from the mill outlet. In general, in order to increase the grinding efficiency, there may be different types of interconnections between the mills and the dividers.
Generally speaking, the main goals of the grinding process can be to obtain the output materials of the same and the desired size as the final product without causing other impurities, such as metals or other contaminants inside it, to increase whatever The greater the power of the grinding circuit and, ultimately, the reduction of production costs in the overall process of work.
For this purpose, various mathematical models and highly applied and highly developed control methods are used to achieve these goals. We intend to review in this article a brief overview of the basic principles in the modeling of grinding process and the analysis of various strategies for controlling the design of the control structure and, finally, we can propose a suitable process control method.
- Modeling of the process
II.1. Basic fragmentation mechanisms
In order to achieve a specific mathematical relationship between feed size and final product size, the main idea in the modeling of all crushing processes, including the grinding process, was unveiled.
However, over time, the main raw material or chopped feed used during the production process is reduced to a small extent because the imparting energy of the grinding media creates a disturbance in their bonding forces.
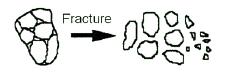
This size reduction is the result of one of the three fragmentation mechanisms described below.
- When local low tensionstress occurs, the abrasive process is applied, and due to this wear, particles that are attached to larger pieces, so-called mother particle, are taken of theirmother and particles that are approximately the same size as the mother particles also are taken. (figure 2a)
a b
c
Fig. 2
- When intense stresses occur slowly but relatively (compression) during the milling process, particle cleavage occurs, which results in the production of parts in the range of 50-80% of the actual size of the primary particles. (figure 2b)
- The result of the rapid use of intense stresses or severe impact is the formation of fractures, which makes the pieces relatively small in shape and with a fairly large distribution of particle size (Fig. 2)
Of course, it should be kept in mind that in practice each of these three different mechanisms never happens alone, and issues such as type of mill, different operating conditions, or type of ground material can be involved in the process of reducing particle size and possibly overcoming one of these three mechanisms to bring.
Typically, several main concepts are mostly used in modeling the grinding process. What defines different size classes is certainly the presence of raw materials that naturally consist of particles that are significantly different in size.
For quantitative measurement of the particle size in each class, measurements from standard sieves are used. In general, solid state theory is used in a series of stages in the segmentation process, with two main operations:
(i) First, you must select a piece of material that is supposed to be broken
- Secondly, by breaking the materials selected for production reach to distribution of the fragment sizes.
The two structures that can be identified with these operations are: the selection function Si in this function Si, i=1, 2, …, n, and the breaking function bij, n ≥ i ≥ j ≥ 1. In this function, n denotes the number of classes of size. The breakage function or specific breakage rate, which is the Si choice function, is intended to represent the probable size of the Xi Particles in each step, the piece given to the machine for milling is considered, and in this function xi is the lowest possible particle size.
In addition, S1, S2, …, Sn are the mass of material in different classes, the initial sizes given to the machine to be milling and converted into smaller particles. The breaking function of bij which, of course, it can also be called the distribution function, essentially describes the distribution of the size of the pieces obtained after grinding or breaking particles in size Xj.
As a result, b1j, b2j, …, bnj is the mass fractions of particles after breaking the particle in the size of the class j, which in fact corresponds to the particle masses obtained in classes 1, 2, …, n.
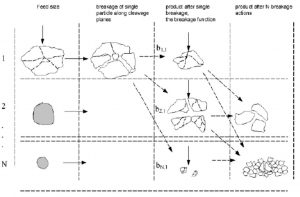
Generally, in Fig. 3, the fracture mechanism of the particles is shown graphically. In the left column, the initial feed size distribution is shown to the device. Then, using solid arrows, the application of forces on particles is shown in different classes of sizes, and the use of point arrows to move parts is to the same or lower size of classes.
In the third column, it is also attempted to show breakage functions, and finally, in the fourth column, products that are eventually obtained with a number of diminishing sizes are shown. During this process, in lower-level categories, the feed mass in the class size 1 is distributed.
Then, by breaking down the particles and distributing them in smaller dimensions at a specified time, the mass value of 1 is completely eliminated. But ultimately, the whole mass will remain constant.
Fig. 3
It should be kept in mind that the basic parameters in the modeling of the selection function and the breaking function are that they have communication processes. In general, three types of models are accepted in the literature: matrix, kinetic and energy models.
For the development of each model, a special principle has to be given to a general principle, including establish mass balance or energy balance equations that are related to the mass or energy components involved in the process. Matrix models should be used at times when the size reduction is largely a discrete process with each discrete step containing three selection-breakage-classification.
Remember that when it comes to a continuous steady state mills for batch milling modeling, reducing the size of a continuous process should be considered as a continuous process in which case the model Mathematics deals with time-dependent parameters and considers the time of work. In this case, kinetic models and energy models are more likely to be used than matrix models.
II.2. Kinetic and energy models
Different types of grinding mills and milling circuits have different assumptions when modeling the grinding process. Generally, the basic assumption is that the milling content is uniform and is completely mixed with the milling rotation as well as the displacement of the grinding media. For this reason, we call this model a totally complex model or perfectly mixed model.
But sometimes the grinding of the mill is completely mixed in the direction of radial direction, but it is not mixed in full axial direction. The second important assumption is that particles in different sizes are broken down in the normal or in the same way, and during this process, the reduction in the size of the raw material, no agglomeration process occurs.
Accordingly, we use kinetic models in grinding processes that are based on our mass-balance equations for describing the process at different size intervals. Assuming that the mill is completely mixed in the radial direction and is somewhat mixed in the axial direction, then the kinetic model of second order is given should be used more often. So you should use the following form:(1)
dwi ( l , t ) = − S i wi ( l , t ) + ∑i−1 S j bij w j ( l , t ) + D i d 2 wi (2l , t ) − ui dwi ( l , t ) ,dtdldlj=1
In this form:
t indicates the mill time;
l – Represents the spatial coordinates in the axial direction of the mill;
wi (l , t) – Indicates the mass fraction of material in the i-th size class
bij –Grinding Break Function;
Si – Grinding selection function;
Di – Milling mix Coefficient;
ui – Indicates the speed of material transport in the axial direction of the mill
To illustrate the change in the value of the material mass fraction in the size class i at a time interval [t, t + dt], the left side of the equation is used.
On the right, the first and second terms are used to indicate the mass of particles disappearing and appear particles in this class. In the third term, we describe the degree of axial dispersion, and in the last or fourth term, the convective transport of particles in axial direction is shown at the velocity ui. The differential equation (1) has the following boundary conditions:
Here fi (l ) represents the mass of feed fraction in the size class i and l is the length of the mill
With conditions 2-4 in Equation 1, we are actually showing the basic kinetic model of the process. Of course, this kinetic model has a number of well-known models that determine the specific operating conditions of the mill.
It is generally assumed that the charging is completely mixed and is completely uniform in both axial and radial directions, which is why the fully mixed model is used. In this particular case we can ignore the third and fourth terms in Equation 1 and design the kinetic model of the mill in the following form [3, 25, 46]:
| Here’s is the diagonal matrix of composite elements si | i = 1, 2, …, n, | B is a smaller | |||||||||
| triangular matrix | with component bij , | n ≥ i > j ≥ 1, w(t) is | a | direct with component | |||||||
| wi (t ), i = 1, 2, …, n, | and I shows the identity matrix. Matrix (B − I )S | in (6) has a | |||||||||
| less triangular | form with | oblique component −S1 , − S 2 , …, − Sn . | Under the | ||||||||
| supposition that functions bij | and Si | are known and time independent, the resolving | |||||||||
| of (6) is give by | |||||||||||
| where exp[(B − I )St] is the | matrix | exponent and w(0) is | the vector of initial |
In the class size, the conditions with the elements equal to the mass of the feed. The proper and precise formula for wi (t) i = 1, 2, …, n, is known as the Reid solution used for the batch mill equation and is shown in [3, 23].
In the modeling of grinding process, the cumulative form of Equation 5 can also be used. for example:
is the cumulative fractional mass fraction of particle that have a size larger than xi and is smaller than the size of the particles of class i.
For the pre-supposes, a basic knowledge of the breakage and selection functions bij and Si, we can use the solution obtained in the solution of equations 5 and 8.
Although it is better to refer to experimental processes and successive therapies for certain processes, and, of course, to obtain totally experimental results, since these basic functions are not very well known in these topics. In general, there are many methods for determining breakage functions and some typical breakage function diagrams. In an explicit form, the cumulative equation of grinding 8 is also shown in 3.
To describe the grinding process, you can even use mathematical models based on energy-balance equations. In model 21, a linear model that is similar to model 5 is used, which has been further developed, in which we chose the batch milling kinetics for a particular energy as an independent variable and instead of milling time.
Some researchers have worked out a series of precise and specific tests to measure the specific energy consumed by ball mill in different situations and operations and in different ground material. The results obtained in the dry mill condition and the analysis of these results showed that the size-discretized breakage rate functions with the specific energy entering the mill and the distribution functions of the breakage can be constant and the same. Therefore, in such a structure, the equations modeling related to the energy balance can be represented by the following grinding model:
| the | is the energy-normalized breakage rate parameter and | ||||||
| SiE | |||||||
| E is the specific energy entering to the milldefined as | Si | ||||||
Note that in Equation (10) we consider p as the input of power to the mill and W as the mass of the feed material in the mill.
In the following, we will give a simple comparison between the mass balance model presented in Form 5 and the energy balance model presented in Form 10. Equations 5 and 9 are both linear models, and are relatively simple and easy to use and have a high degree of kinetics for studying first-order breakage kinetics in the process.
We studied the model 5 perfectly, and we obtained the solution of differential equations in clear and explicit forms in literature under various hypotheses and degrees of approximation. Generally, in Form 5, the change in the particle size of the ground material was recognized as a solution in the milling time function.
On the other hand, instead of the exact time of analysis, we can estimate the breakage kinetics with respect to the specific energy consumed in accordance with model 9.
In addition, in order to use the measured data as a fully functional control parameter in the process, it is possible to measure the input precision of the power to the mill. On the other hand, in the milling scale and in the analysis of other comminution systems such as roll mills, the use of the model referred to in 21, which is an energy model, can be very useful. Of course, apart from linear models, more-developed and mathematical-based models can be used in the process of grinding, including nonlinear, time-dependent selection and breakage functions [7, 20].
Among other methods that are often used to study the dynamic properties of the damaging process, the computer simulation method is based on a discrete element [31, 32, 38].
III. Process control methods
Factors such as the non-linear and uncertain character of the process, along with possible errors in the mathematical model, the presence of the variables of the process of interacting with different dynamics, as well as the influence and effect of unwanted disturbances and excessive time delay and violent practical conditions, and ultimately the inability to use tools such as Accurate and reliable sensors make controlling a grinding machine a very difficult task.
In addition, this process is very important in order to achieve factors such as increasing the output power of the circuit and the quality of the final product, as well as minimizing the cost of production to achieve this process and efficient control of this process.
III.1. Process variables and characteristics
If we look at the control point of view, the grinding circuit of a ball mill should be a process with a multivariate interconnected system that has strong interactions between the process variables.
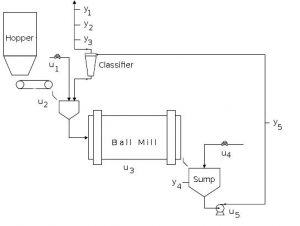
For example, in a simple and ordinal structure, the closed-loop circuit of a wet grinding can be consisted of a ball mill, a sump and a divider [10, 13, 33, 39], as shown in Figure 4.
Fig. 4
In the above figure, there are several process input variables that include:
u1: water flow rate of mill feed
U2: feed rate of fresh ore
U3: speed fraction in the mill critical
U4: rate of water flow of sump dilution
U5: flow rate of sump discharge
The values of these variables are used to control the output variables listed below and are shown in the figure:
Y1: The mass fraction of products or feed given with smaller particle sizes than the quantities available
Y2: Concentration of product solids
Y3: product flow rate
Y4: sump’s slurry level
Y5: Concentration of sump solids
In this process, with some possible abnormalities, we will also be justified that the most important ones that can affect the process are the ore hardness changes as well as changes in the size of the feed. We can write in the form of a matrix form below this model, which is a type of input-output process:
| (11) | … | ,
|
| where | is the transfer function relating the i-th input and j-th output for |
i, j = 1, …, 5.
In these circumstances, they usually try to determine the transfer functions by using the test of the steps changes of the input step and, of course, measuring the output response.
Of course, achieving accurate and correct results usually requires a lot of experiments. In addition, topics such as configurations and grinding circuit equipment are factors that may require different sets of input and output variables to design their own model [8, 33, 40].
Typically, controlling the process of a ball millgrinding circuit is facing a lot of problems, the most well-known and most important of which are as follows:
- Ball mills have a nonlinear process that has both immeasurable disturbances and no model for dynamism.
- The interconnections between the variables is very strong, so that each of the input variables is associated with at least several output variables.
- A large number of process time constant can be seen, while some input / output pairs are time-consuming.
- The system model of the ball mill has many integrals.
- In the process of parameters, the time is varying as the age of the circuit
- Sometimes there are technology constraints in this process that can be seen on manipulated and controlled variables
- Ultimately, the measure cannot be completely trusted and noisy.
In general, the general objectives of the control can be further described as follows: first, the constant output variables should be maintained at the set-fixed point, because at this stage our goal is very important to be able to measure the distribution of the stable product size as the percentage of output materials with particle size less than the measured value.
In the whole process, and in succession, one of the optimization problems of this goal will be control objective, which should be provided as a performance criterion, and this should be done with certain restrictions. This can help minimize production costs by maximizing the output of the grinding circuit. Having different and varied constraints in optimization problems, minimum or maximum values of the inputs, output and internal process variables affect the limitations of equipment, operational safety equipment, or environmental regulations.
It seems that for many control methods in practice one of the challenging problems is to design a control system for grinding, since this process itself has the inherent characteristics and constraints of the process. In the following, we will look at two of the methods that will usually be used, and with a simple analysis, we will explain the advantages and disadvantages of these methods.
III.2. Decentralized control
According to the results of a statistical study [48], decentralized control is often used in ball mill grinding circuits. In general, it can be said that the convenient distribution of control and easy implementation of this method are its main advantages.
Typically, these types of structures consist of several single-input single-output loops that include several different processing variables.
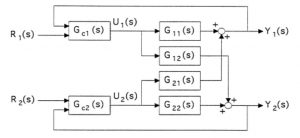
In Figure 5, the diagram of two-input two-output system is shown, in which the transfer functions are two open loops with connections are represented by ………… 1,2 and the controller structure transition are. ……. and …….
Fig. 5
In [35], for the design of extended PID controllers, a frequency-based method is described in which the transmission structures are determined and identified in the form
(12) , .
Regarding the interconnected system in (12), we can say that individual adjustment from each controller depends on other parameters. Therefore, in order to overcome this problem, we have begun to design a precise method specified in [35] to determine the value of the closed loop system.
In designing a proper distribution grinding process control, one of the most difficult cases is always selecting the right pair for manipulated and, of course, controlled variables. The reason for this is that with the mistake of choosing the right input-output pair, the desired balance between the control loops will be lost and, as a result, poor control will be controlled.
There are many methods for selecting the proper input and output pair, which shows the two common types of variables in the grinding circuit system with a sump and a hydrocyclone classification in Table 1[13].
Table 1
| Pairing | Controlled Variable | Manipulated Variable | |
| I | hydrocyclone overflow Particle size | Rate of Sump water dilution | |
| Rate of hydrocyclone feed | rate of fresh solids feed & dilution | ||
| II | hydrocyclone overflow Particle size | rate of fresh solids feed & dilution | |
| Rate of hydrocyclone feed | Rate of Sump water dilution | ||
After analyzing dynamic responses to a determined point change in the size of the product, it was found that in both cases of pairing I and pairing II there is a relationship between the control loops. According to the analysis of both steady state and dynamic behavior, the appropriate selection of controlled pairs was manipulated because of strong interactions between variables.
The current control theory for more than two inputs and two output variables is an appropriate and valuable tool, and it can easily be used to manipulated control pairs that are used for the relative increase technique.
In relation to the system, in this method, a relative gain array is used, and for the selection of pairs, it is also based on the analysis of the structure and properties.
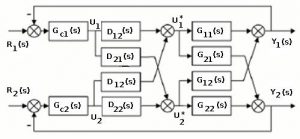
In order to compensate for system interactions in a decentralized control structure, there is also a different approach and methods that is widely used and also includes additional separation controllers between the control loops of the system. In Figure 6, you will see an image of a system with a control loop and a separator or decouples in which the transfer functions of the separator controllers are used.
Fig. 6
In this system, using the vector matrix equations, we describe the input-output equation.
where
| , | ||||||||||||
| where | 0 | |||||||||||
| , | , | , | . | |||||||||
| 0 | ||||||||||||
| Given that a diagonal matrix is used, we look for the transfer functions of the decoupling controllers in a way that determines that the diagonal matrix
|
||||||||||||
| 0 . | ||||||||||||
| 0 | ||||||||||||
| From (15), we have | 0 | |||||||||||
| . | ||||||||||||
| 0 | ||||||||||||
| If | and | are determined as | det | / | and | det | / , | |||||
Then, from Form 16, the transfer functions of the decoupling controllers can be obtained by form
| 1, | 1, | , | . |
III.3. Multivariable control
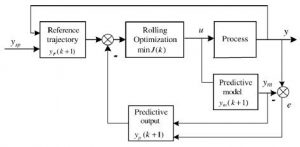
It is usually recommended to use Multivariable control methods in complex industrial processes that have strong interactions between their variables. For this reason, we have managed to use a Multivariable approach based on the model control prediction strategy (MPC) in controlling the ball mill grinding circuits [26, 33, 39].
This approach can be used for a wide range of industrial applications in which the control is designed in such a way that the process is directed from a one constrained steady state to another constrained steady state. The general objectives of the MPC system are outlined as follows.
- in order to eliminate violations of input and output restrictions in the process
- In order to control the variables, we can direct them to arbitrary values of their steady-state optimal or optimize the so-called dynamic outputs.
- In order to direct the manipulated variables to their arbitrary and desirable levels of steady-state optimal, which can be used in terms of the remaining degrees of freedom or optimize dynamic inputs.
- In order to prevent excessive movement of manipulation of variables
With the aim of maximizing plant control as much as possible in the event of failure of all signals and actuators.
In general, the MPC has a control structure that includes an internal process model and a prediction control computation. To predict the future output of this process we should use of an internal model. By solving a limited horizontally optimized problem in order to minimize the differences between the desired reference path and the output that is predicted, future actions of the manipulated variables can be determined.
In each sampling interval, the optimal problem must be solved to be used as a solution to a sequence of future actions. In the next steps, the procedure is repeated and only the first controller factors are applied at sampling intervals. In the reference [37] we used a MPC approach to investigate a comprehensive review of algorithms.
In Reference [14], we can conduct a daily review of the current operation and possible challenges of the MPC in order to provide a simple representation of the MPC theory in a monologue [16].
One of the main methods of MPC, which was unveiled and developed in the late 1970s in the last century, is the use of the Matrix Dynamic Control algorithm (DMC). This methodology was first used for the petroleum industry. Following this algorithm was used to control the process in the ball mill grinding circuits of different ball mills using control strategies using the DMC algorithm that was a powerful and efficient tool [8, 10, 39].
In [8], as shown in Figure 7, the implementation of the DMC algorithm is presented.
Fig. 7
| If Indicates the length of the projection period of the prediction output, followed by the predicted output | ||||
| vector | T | |||
| 1 | 1 , … , | |||
| is obtained as | ||||
| (18) | 1 | 1 | , | |
| where | 1 | 1 , … , | T | is the model output, G0 is a |
coefficient matrix and
indicate the distinction between the process and model output vectors. The predicted control vector is in the form
| ∆ | ∆ | , …, ∆ | 1 | T, | |||||
| where M is the length of control prediction | horizon. The | values | of | ∆ | are | ||||
| difined by a minimization of the following second-class objective function [8] | |||||||||
| (19) | 1 | 1 | T | 1 | 1 | + | |||
| ∆ | T | ∆ | , | ||||||
| here the weighting coefficient matrix is an output and | is | a control | weighting | ||||||
| coefficient matrix. Process limitations variables are shown in the form | |||||||||
| , | 0, 1, … , | 1, | |||||||
| ∆ | 1 | ∆ | , | 0, 1, … , | 1, | ||||
| , | 0, 1, … , | 1. | |||||||
The correct selection of the values of the parameters for controlling the process in the correct use of the MPC algorithm is very important for the ball mill grinding process, so the choice of values such as the length of the projection horizon of the model output, the length of the control prediction horizon, the coefficients of the outflow weight and the input of the manipulation of the variations should be very careful.
Generally, the length of the output prediction horizon will take so long as it can capture the behavior of the steady state behavior of the output.
Regarding the M-prediction horizon, we know well that what improves control performance is actually an increase in M, but increasing the amount of computation can be as price. The point is that it is primarily M shorter than P. Secondly, what determines the weight factor in performance is the desired output behavior along with the cost of control.
If we want to control some of the output variables more precisely, we need to calculate it with a value above the appropriate weight. Although the image of this issue is also dominant, when increasing the variables of manipulation too much, the increase in the values of controlling weight coefficients will suppressed.
Following the simulation studies and practical application of multivariate and decentralized control systems in the ball mill grinding circuits, the following results were obtained in two control strategies.
- Simplified implementation of the control system in a decentralized system with a local PI or PID controller will overcome practical applications. In single-input single-output control loops, the process variables are coupled. For example, for a controlled variable, a manipulated one is used. There are, of course, problems with this method, such as selecting the appropriate variable pair and separating control loop interactions with proper adjustment or by introducing separation controllers. On the other hand, the multivariate approach will prevent complex problems with the cost of a more sophisticated control system.
- According to reports in the literature, the use of the MPC algorithm in multivariable methods is increasingly popular with the successful implementation of this method. In fact, the ability of this method to counteract the strong interactions between process variables, as well as the ability to control the control system is one of the great benefits of this method. However, at the design stage, there should be a detailed modeling for the MPC algorithm, and requires very detailed and complex computations in the overall process control.
- In decentralized PID controllers, though, constant state errors and closed loop responses are considered in small changes made in a pair of appropriate variables, as well as control pairs between pairs, but the results are always satisfactory. Although simulated studies yielded results that showed significant benefits from MPC compared to the decentralized PID controllers. In addition, the technological constraints of manipulated and controlled variables are well thought out explicitly in MPC designs, which allows the optimal operating conditions of the control system to be obtained. In addition, the problems associated with unwanted disturbances, time delay and nonlinear process of the process of comfort and success in this approach are overcome.
- In the process of a special ball mill, both the choice of control method and the structure of the control system should normally take into account certain economic value indices. In general, it seems more difficult to estimate potential economic gains in structures with more complex control and more difficult computing than using simple control schemes. Of course, we should note that this research is only for examining the distribution of particle size in a ball mill process, which is why we conclude that due to the moving point to the operating point, the profit from this type of operation is better than larger profit. Which requires more complex and accurate processes. In total, it can be said that in the process of industrial ball mills, energy efficiency and economic evaluation should be introduced as a serious and unplanned problem, which requires a lot of research in the future and comprehensive studies [2, 19, 26, 27, 48].
At the end of this research, we are going to point out a number of other advanced techniques that can be used to control the process in the ball mills. In [24], an approach was simultaneous decoupling of interactions and closed loop pole assignment at the same time.
In [50], the control system including observer disorder and MPC was investigated. In [43], we described the innovative control systems and compared PI multivariate, fuzzy, and prediction control models.
In [34], a comparative control method was introduced that could be used in the grinding process. In [9, 11, 12], we generalized the simulation results with a specific system control system, monitoring control and observational control.
In [41], we introduced an integrated automation system for grinding process control, and finally, a neural control approach was introduced and developed in [13].
In the grinding process, we can only design mathematical models based on mass balance or balance of energy equations that these models can help us to calculate the particle size reduction factor as the mill time function or the amount of specific energy consumed.
In both cases, selection structures and breakage functions are considered as the main parameters, with no title being prioritized, and other studies and experiences should be considered for the determination of these structures.
The development of more accurate and more complicated mathematical models, including nonlinear mathematical models, and the choice of suitable time variables and breakage functions, are a subject of interest to process modeling.
To control the process, decentralized control methods and multivariate control method were used and simulated in the simulation results. However, more sophisticated control techniques such as a variety of adaptive, specialized, and fuzzy logic control systems are used every day in theoretical studies and simulation of control systems.
There are also many open-source research questions that need to be done to further improve the efficiency of the grinding process, in order to better assess the economic control of a more precise process, and in this context, individuals and researchers interested in gaining more influence are needed.
چقدر این پست مفید بود؟
روی یک ستاره کلیک کنید تا به آن امتیاز دهید!
میانگین امتیاز 5 / 5. شمارش آرا: 7
No votes so far! Be the first to rate this post.